- IPv6 est la norme du protocole Internet (IP) de la prochaine génération, destinée à remplacer à terme IPv4, le protocole que de nombreux services Internet utilisent encore aujourd’hui.
- Le nombre total d’adresses IPv4 est d’environ 4 milliards. Le nombre total d’adresses IPv6 est de 2 à la puissance 96.
- La visualisation de la taille et de la différence de ces deux chiffres permet de montrer la raison, la durabilité et la nécessité de l’IPv6 par rapport à l’IPv4.
Récemment, j’ai réfléchi à la manière de visualiser la grande différence entre les adresses du protocole Internet (IP) IPv4 et IPv6. La difficulté réside dans l’énorme différence d’échelle entre les deux, qui est si grande qu’il est difficile de la représenter clairement.
L’IPv4 offre environ 4 milliards de valeurs distinctes, représentées par un champ d’adresse de 32 bits. Cela signifie 4 294 967 296 valeurs distinctes. En disant “4 milliards”, nous simplifions en excluant environ 294 millions d’adresses, et en disant “294 millions”, nous en excluons encore près d’un million. Nous omettons donc beaucoup de détails lorsque nous parlons de l’IPv4.
L’IPv6, quant à lui, représente 2 puissance 96 adresses possibles de plus. Cette différence, qui se situe entre 2 puissance 128 et 2 puissance 32, se traduit par un nombre stupéfiant de 79 228 162 514 264 337 593 543 950 336 adresses possibles. Le simple fait d’essayer d’énoncer ce nombre semble absurde. Il s’agit d’un nombre à 29 chiffres, et des mots comme “quintillion” ou “jintillion” ne lui rendent pas justice.
Les analogies peuvent aider
Normalement, je ne suis pas un fan des analogies. Elles ont tendance à s’effondrer rapidement. Mon analogie habituelle, un train à vapeur (je suis un vieux passionné de trains), ne fonctionne plus très bien de nos jours, car les jeunes générations les rencontrent rarement en dehors des musées. Mais les analogies sont précieuses lorsqu’elles suivent les lois mathématiques et physiques. Si nous pouvons trouver une situation dans le monde réel qui reflète la différence entre IPv4 et IPv6, cela vaut la peine d’y réfléchir. Et je pense en avoir trouvé une qui fonctionne bien.
L’espace est grand. Très grand.
J’aime comparer la différence entre les espaces d’adressage à la taille relative des objets astronomiques. Cette comparaison est utile car elle nous fait passer des nombres linéaires (de zéro à 4 milliards) aux volumes, les étoiles étant à peu près sphériques. Les sphères sont utiles parce que leur volume augmente plus rapidement que leur rayon.
Volume et rayon
La formule du volume d’une sphère est V = 4/3 π r³, où V est le volume et r le rayon. Si l’on considère le rayon d’une sphère et que l’on compare différentes sphères en fonction de leur rayon, leurs volumes changent de manière significative :
- Une sphère d’un rayon de 1 unité a un volume d’environ 4,19 unités cubiques.
- Une sphère d’un rayon de 2 unités a un volume 33 fois plus grand.
- Une sphère d’un rayon de 10 unités a un volume 4 000 fois plus grand.
- Une sphère d’un rayon de 100 unités a un volume 4 millions de fois plus grand.
Peut-on trouver une “unité” de comparaison ?
Au lieu de considérer tous les bits de l’espace d’adressage IPv4, concentrons-nous sur la partie qu’un fournisseur d’accès à l’internet (FAI) attribue à un client. En IPv6, l’espace d’adressage de 128 bits est souvent considéré comme un espace d’adressage de 64 bits lorsqu’il est question des sous-délégations aux clients, ce qui est une pratique courante dans de nombreux réseaux. Un sous-réseau IPv6 typique utilise une frontière /64 correspondant à une seule adresse IPv4. Cela simplifie les choses pour la comparaison, car la limite du sous-réseau dans les réseaux domestiques est généralement un /64.
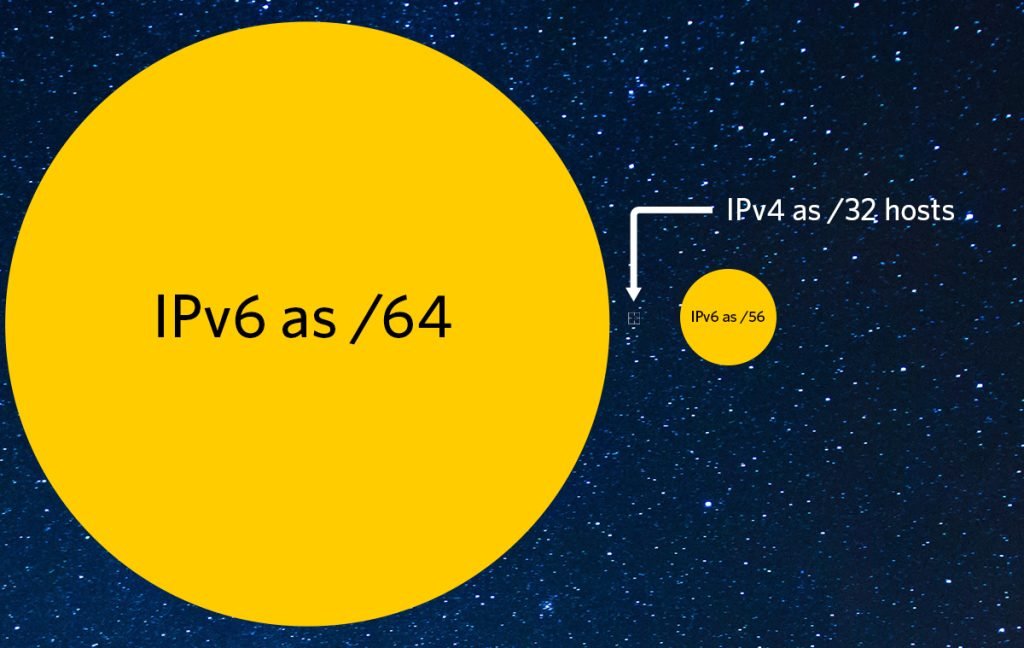
Considérez le rapport entre un /64 dans IPv6 et un /32 dans IPv4. La comparaison est de 2^32, soit environ 4 milliards de fois plus grand.
Comparaison des sphères
Pour mettre cela en perspective, nous pouvons imaginer une sphère 4 milliards de fois plus grande que la sphère “unité” d’origine. Cette sphère aurait un rayon d’environ 1 008 unités. Cette taille correspond au même rapport entre un /64 dans IPv6 et un /32 dans IPv4.
Visualiser l’échelle
Si vous pensez à ces deux sphères, l’une représentant IPv4 et l’autre représentant IPv6 avec un rayon 1 008 fois plus grand, vous pouvez imaginer combien il y a plus d’espace dans IPv6.
Pouvons-nous faire mieux ?
Une autre unité utile dans l’IPv6 est le /56, souvent utilisé dans les réseaux à large bande pour attribuer aux clients un plus grand nombre de sous-réseaux, généralement 256 /64 différents. Nous obtenons une échelle plus réaliste si nous considérons le /56 comme l’équivalent de l’adresse IPv4 unique.
En gardant cette échelle à l’esprit, nous pouvons imaginer la sphère comme un tout.
Existe-t-il des étoiles aussi grandes ?
Il est intéressant de noter qu’il existe dans l’univers des étoiles qui correspondent à ces tailles relatives. Par exemple, Epsilon Pegasi, une étoile de la constellation de Pégase, a une taille comprise entre 169 et 185 fois celle du Soleil. Cela correspond assez bien à la comparaison /56.
Lorsque nous ramenons l’échelle à /64, nous observons des étoiles environ 1 008 fois plus grandes que le Soleil, qui sont généralement des supergéantes rouges. KW Sagittarii, une supergéante rouge dans la constellation du Sagittaire et l’une des plus grandes étoiles connues, est un bon exemple de ce type d’étoile.
Ces étoiles sont massives et lointaines, ce qui nous rappelle l’immensité de l’espace d’adressage IPv6 et la probabilité de l’épuiser.
Adapté de l’article original paru sur le blog de l’APNIC.
George Michaelson est chercheur principal à l’APNIC.