Améliorer la résilience de l'internet grâce à l'analyse spatiale
En bref
- Les données recueillies par la foule sont essentielles pour mesurer la résilience de l'internet au niveau local, mais une couverture limitée peut constituer un défi.
- L'analyse spatiale permet de transformer des données éparses en une carte régionale cohérente des performances de l'internet.
- Une nouvelle étude montre qu'une combinaison de techniques statistiques peut donner une image plus claire des performances locales de l'internet que l'utilisation du recensement ou des limites du quartier ( ).
Une connexion Internet fiable est devenue une nécessité pour le travail à distance, l'apprentissage en ligne et les loisirs. Pourtant, les performances de l'internet varient considérablement en fonction de l'endroit où nous vivons. Il est essentiel de comprendre ces disparités au niveau local pour assurer la résilience de l'internet.
Ookla Speedtest et M-Lab fournissent des ensembles de données collectées par la foule pour comprendre les performances de l'internet. Ces ensembles de données donnent un aperçu de diverses mesures, telles que la vitesse, la latence, la gigue et la perte de paquets, grâce à des mesures effectuées à l'initiative des utilisateurs.
Selon le moment et l'endroit où les utilisateurs effectuent des mesures, la couverture est loin d'être continue. Par conséquent, de nombreuses zones doivent encore être échantillonnées et les données collectées peuvent être bruitées en raison des différences entre les appareils, les heures de la journée ou les conditions du réseau.
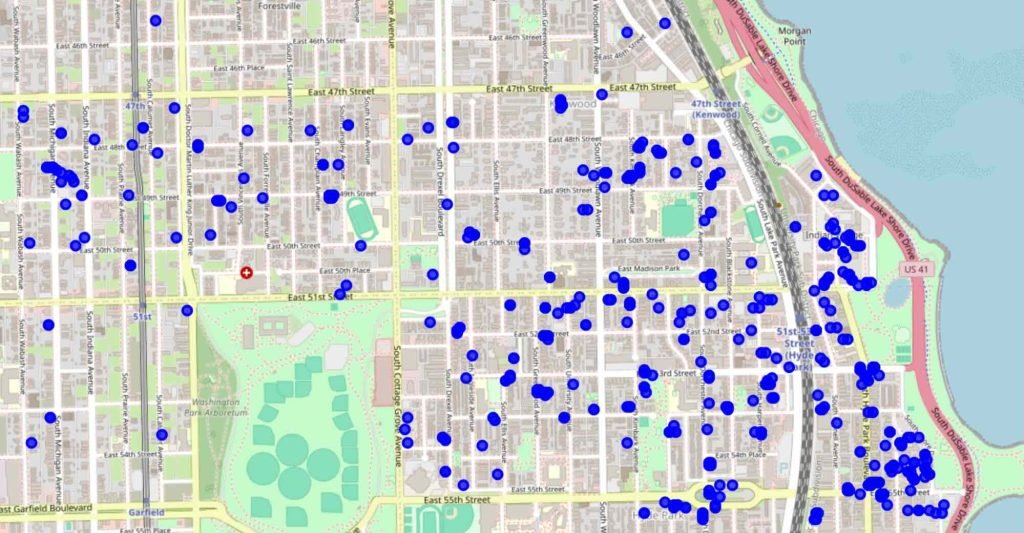
Malgré ces difficultés, les données collectées par la foule peuvent donner des indications sur les domaines dans lesquels l'internet doit être amélioré. En plus de fournir une évaluation de la performance de l'internet à partir d'un grand nombre de points de vue, les données collectées par la foule constituent une alternative rentable aux campagnes de mesure spécialisées. Cependant, leur analyse efficace nécessite une stratégie pour combler les lacunes des données et comprendre les modèles géographiques.
Les frontières axées sur les mesures ne sont pas alignées sur les frontières administratives
L'analyse spatiale permet de surmonter ces difficultés en transformant des données éparses en une carte régionale cohérente des performances de l'internet. Les approches traditionnelles s'appuient sur des frontières préexistantes telles que les codes postaux, qui ne correspondent que parfois au fonctionnement de l'infrastructure Internet. Par exemple, une partie d'un quartier peut bénéficier d'un excellent service tandis qu'une autre souffre de mauvaises performances. Le simple calcul de la moyenne des données peut masquer ces variations importantes.
Nos recherches visent à améliorer l'évaluation des performances de l'internet en définissant des limites d'échantillonnage géographiques qui reflètent les variations réelles des performances. Cela est particulièrement important pour mesurer la résilience de l'internet, c'est-à-dire lacapacité d'un réseau à maintenir ses performances en cas de forte demande, de pannes ou d'autres perturbations. En identifiant les zones de mauvaise performance persistante, nous pouvons mieux cibler les investissements pour améliorer la résilience du réseau.
Nous utilisons un processus en trois étapes pour déterminer des limites géographiques significatives.
- Nous interpolons les données existantes afin d'estimer la performance de l'internet pour les lieux non échantillonnés.
- Nous superposons de petites grilles hexagonales pour agréger les performances.
- Nous utilisons des techniques de regroupement pour définir des limites qui représentent des régions aux performances similaires.
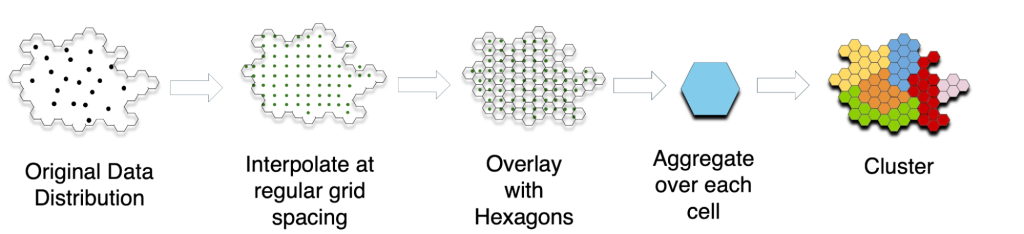
Cette méthode nous permet d'identifier les zones contiguës où le temps de latence est particulièrement élevé (figure 3). Le temps de latence est crucial pour des applications telles que la vidéoconférence, les jeux en ligne et la navigation sur le web, ce qui en fait un bon indicateur de la qualité globale de l'internet.
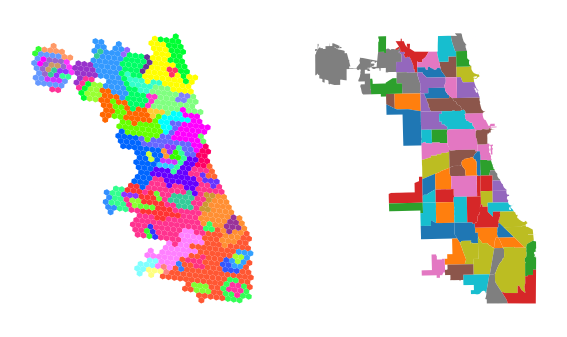
Dans le cas de Chicago, nous n'observons pas de correspondance univoque entre les limites administratives et les limites fondées sur les mesures pour le même nombre d'unités spatiales (N = 77). Ces résultats suggèrent une différence significative par rapport aux études antérieures qui utilisent les limites administratives pour agréger les données de performance Internet. Nous recommandons l'utilisation d'une interpolation préalable et d'unités spatiales à haute résolution pour les analyses orientées vers la politique.
L'interpolation préalable réduit la sensibilité aux choix d'unités spatiales dans les résultats agrégés
Nous mesurons la similarité entre 17 regroupements mensuels des données fournies par la communauté en utilisant l'indice Rand ajusté (ARI), mesuré sur une échelle de -1 à 1, où :
- -1 = désaccord maximal
- 0 = assignation aléatoire des limites
- 1 = accord maximal.
Si nous effectuons un simple calcul de moyenne sur des mesures dispersées, le choix des unités d'agrégation géographique affecte la similarité des frontières dans le temps (figure 4). Cependant, le choix de l'unité d'agrégation a moins d'impact lorsque nous calculons la moyenne des estimations de latence interpolées sur la grille - de petits hexagones pour l'agrégation entraînent une plus grande similarité des limites dans les deux cas. Un ARI médian de 0,59 pour la moyenne interpolée avec des hexagones réguliers implique une similarité modérée à solide, ce qui suggère que notre approche révèle une structure spatiale significative à travers les ajustements mensuels.
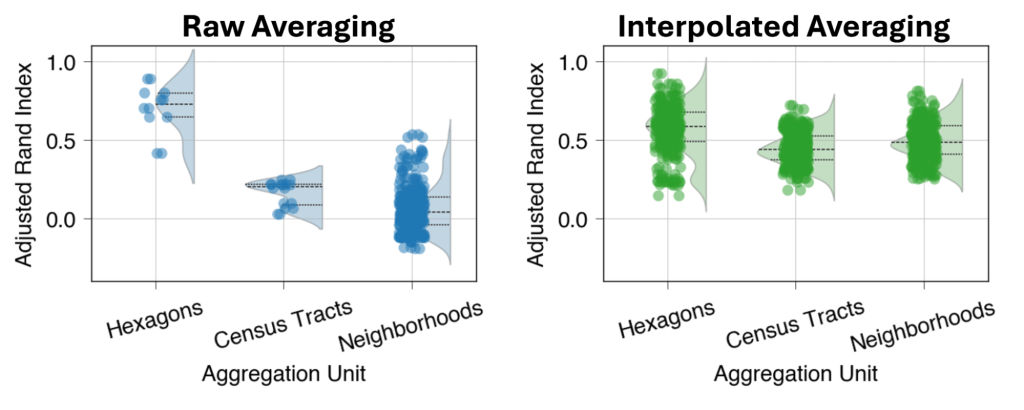
Lisez notre article pour plus d'informations sur nos méthodes et nos résultats.
Taveesh Sharma est étudiant en troisième année d'études supérieures en informatique à l'université de Chicago.
Les opinions exprimées par les auteurs de ce blog sont les leurs et ne reflètent pas nécessairement celles de l'Internet Society ou, en l'occurrence, du Brattle Group.

