Visualizing the Scale Differences of IPv4 and IPv6

Recently, I’ve been thinking about how to visualize the vast difference between Internet Protocol (IP) addresses IPv4 and IPv6. The challenge lies in the enormous difference in scale between the two, which is so large it’s difficult to represent clearly.

IPv4 offers around 4 billion distinct values, represented by a 32-bit address field. This means 4,294,967,296 distinct values. By saying ‘4 billion’, we simplify this by excluding about 294 million addresses, and saying ‘294 million’ still excludes nearly another million. So, we’re leaving out a lot of detail when discussing IPv4.

IPv6, on the other hand, represents 2 to the power of 96 more possible addresses. This difference, which is between 2 to the power of 128 and 2 to the power of 32, results in a staggering 79,228,162,514,264,337,593,543,950,336 possible addresses. Even trying to say this number feels absurd. It’s a 29-digit number, and words like ‘quintillion’ or ‘jintillion’ just don’t do it justice.

Analogies Can Help

Normally, I’m not a fan of analogies. They tend to break down quickly. My usual analogy, a steam train (I’m a trainspotter of old), doesn’t work well these days since younger generations rarely encounter them outside museums. But analogies are valuable when they follow mathematical and physical laws. If we can find a situation in the real world that mirrors the difference between IPv4 and IPv6, it’s worth considering. And I think I’ve found one that works well.

Space is Big. Really Big.

I like to compare the difference in address spaces to the relative sizes of astronomical objects. This is helpful because it shifts our thinking from linear numbers (from zero to 4 billion) to volume, as stars are roughly spherical. Spheres are useful because their volume scales faster than their radius.

Volume and Radius

The formula for the volume of a sphere is V = 4/3 π r³, where V is the volume and r is the radius. If we consider the radius of a sphere and compare different spheres by their radius, their volumes change significantly:

• A sphere with a radius of 1 unit has a volume of about 4.19 cubic units.
• A sphere with a radius of 2 units has a volume 33 times larger.
• A sphere with a radius of 10 units has a volume 4,000 times larger.
• A sphere with a radius of 100 units has a volume 4 million times larger.

Can we Find a ‘Unit’ to Compare?

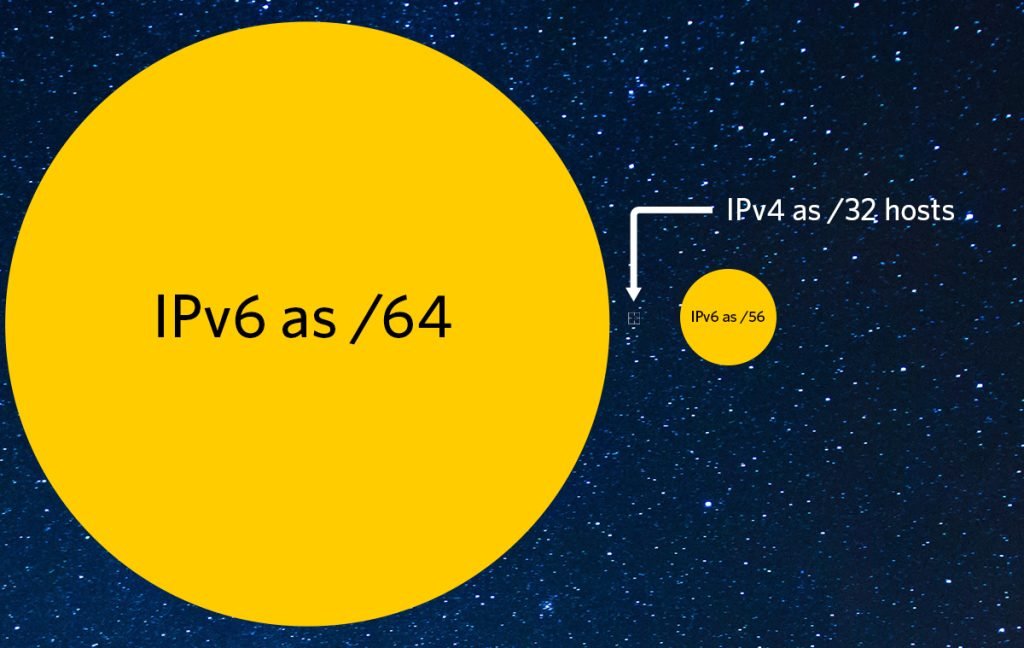
Instead of considering all the bits of the entire IPv4 address space, let’s focus on the portion an Internet Service Provider (ISP) assigns to a customer. In IPv6, the 128-bit address space is often viewed as a 64-bit address space when discussing customer sub-delegations, which is standard practice in many networks. A typical IPv6 subnet uses a /64 boundary corresponding to a single IPv4 address. This simplifies things for comparison because the subnet boundary in home networks is typically a /64.

Consider the ratio between a /64 in IPv6 and a /32 in IPv4. They compare as 2^32, or approximately 4 billion times larger.

Comparing Spheres

To put this into perspective, we can imagine a sphere 4 billion times the size of the original ‘unit’ sphere. This sphere would have a radius of about 1,008 units. This size is the same ratio between a /64 in IPv6 and a /32 in IPv4.

Visualizing the Scale

If you think about these two spheres, one representing IPv4 and the other representing IPv6 with a radius 1,008 times larger, you can imagine how much more space there is in IPv6.

Can we do Better?

Another useful unit in IPv6 is the /56, often used in broadband networks to assign customers a larger range of subnets, typically 256 different /64s. We get a more relatable scale if we consider the /56 equivalent to the single IPv4 address.

With this scale in mind, we can imagine the sphere as a whole.

Are There Stars this Big?

Interestingly, there are stars in the universe that match these relative sizes. For example, Epsilon Pegasi, a star in the Pegasus constellation, is between 169 and 185 times the size of the Sun. This corresponds quite well to the /56 comparison.

When we scale back to the /64, we’re looking at stars about 1,008 times the size of the Sun, which tend to be red supergiants. KW Sagittarii, a red supergiant in the Sagittarius constellation and one of the largest known stars is a good example of such a star.

These stars are massive and far away, reminding us of the vastness of IPv6 address space and the likelihood of exhausting it.

Adapted from the original post that first appeared on the APNIC Blog.

George Michaelson is a Senior Research Scientist at APNIC.

Track the use of IPv6 in your country and globally via the Pulse Technologies and Country Report pages.